Vortrag auf der DPG-Tagung des Fachauschusses ‘Didaktik der Physik’ am 10.3.1997 in Berlin
 

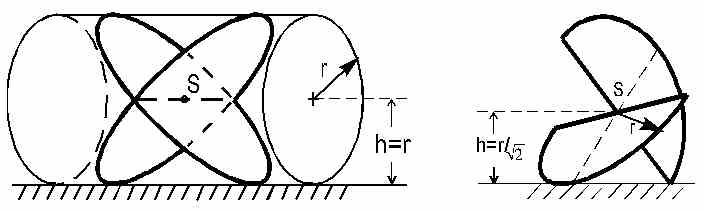
Das zweite Objekt, das ich vorstellen möchte, ist der Zwei-Scheiben-Roller. Wenn man eine homogene Kugel eine leichtgeneigte Ebene hinunterrollt, bleibt der Abstand der Kugelmittelpunkts, der zugleich Schwerpunkt ist, in konstantem Abstand von der Ebene. Das Gleiche gilt für einen Zylinder. Der Schwerpunkt beschreibt beim Rollen eine gerade Linie.

Schneidet man aus einem Zylinder zwei elliptische Scheiben geeignet aus (Abb. 3), bewegt sich der Schwerpunkt ebenfalls in konstantem Abstand und auf einer geraden Linie.

Im rechten Teil von Abbildung 3 sind zwei Halbkreise senkrecht miteinander verbunden. Auch hier bleibt der Abstand des Schwerpunkts von der Ebene offensichtlich konstant. Seine Bahn ist aber keine gerade Linie mehr. Sie ähnelt vielmehr einer Schlangenlinie. Beim Abrollen bewegt sich dieser Zwei-Halbkreis-Roller taumelnd hin und her. Er wird im Englischen deswegen auch Wobbler genannt.

Wobbler

Abb. 3: Zwei aus einem Zylinder ausgeschnittene elliptische Scheiben halten beim Abrollen auf einer schiefen Ebene einen konstanten Schwerpunktabstand zur Ebene. Die Bahn des Schwerpunkts ist eine Gerade.
Bei der Konstruktion rechts sind zwei Halbkreise senkrecht miteinander verbunden. Der Schwerpunktabstand bleibt ebenfalls konstant. Die Bahn des Schwerpunkt ähnelt einer Schlangenlinie.

Der Schweizer Künstler Rolf Hergert hat nach diesem Prinzip ein Objekt geschaffen, das er Go-On nennt (Abb. 4). Es ist aus dem lichtsammelnden Material LISA gefertigt, welches häufig zu Werbezwecken eingesetzt wird. In das klare Plastikgrundmaterial sind fluoreszierende Moleküle eingelagert. Das führt zu dem interessanten Effekt, das das eindringende Licht intensitätsverstärkt an den Kanten austritt.

Go-On

Abb. 4: Der Schweizer Künstler R. Hergert hat aus zwei halbkreisartigen Teilen ein Objekt geschaffen, das er Go-On nennt.

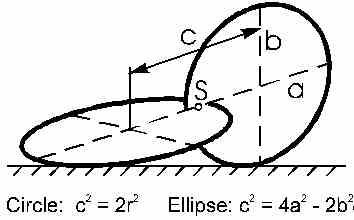
senkrecht zueinander verbundene Kreisschreiben

Abb. 5: Zwei ganze Kreisscheiben, deren Mittelpunkte einem definiertem Abstand c aufweisen und die senkrecht zueinander verbunden werden, rollen mit konstantem Schwerpunktabstand zur Ebene. Das gilt sogar für Ellipsen (a = große; b = kleine Halbachse).
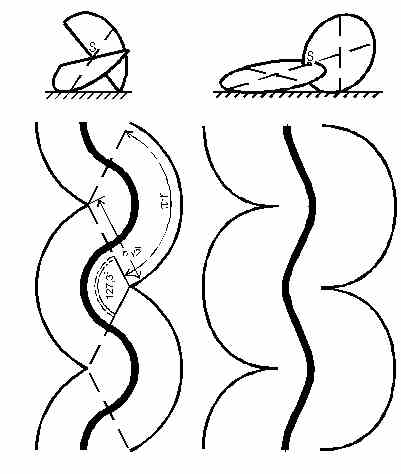
Verbindet man zwei ganze Kreisscheiben senkrecht zueinander, wie das in der Abb. 5 gezeigt ist, ergibt sich für einen - und nur diesen - Abstand der Mittelpunkte der Scheiben ebenfalls, das der Abstand des Schwerpunkts von der Ebene konstant bleibt. Die etwas längliche Rechnung dazu möchte ich hier nicht durchführen [3].

Die Bahn des Schwerpunkts sieht ebenfalls schlangenförmig aus. Bei dem Roller aus zwei Halbkreisscheiben ist diese Schlangenlinie mathematisch ziemlich einfach beschreibbar als aus Teilen von Kreisen zusammengesetzt (Abb. 6).

Beim Roller mit zwei ganzen Kreisscheiben ist die Form dieser Linie bis jetzt nicht bekannt. Vermutlich gibt es keine analytische Lösung.

Das Prinzip des Zwei-Kreisscheiben-Rollers ist in diversen Spielzeugen und künstlerischen Objekten realisiert. Dabei wurde die gerade formulierte Abstandsbedingung manchmal ganz bewußt umgesetzt, manchmal unbewußt sehr genau getroffen, manchmal auch nicht genau verwirklicht. Dafür seien einige Beispiele angeführt.

Bei einem finnischen Kinderspielzeug aus Holz namens Ensihammas (Abb.7) ist diese Abstandsbedingung ebenfalls unbeabsichtigt erfüllt. Die taumelnde Bewegung beim Rollen dieses Spielzeugs scheint sogar Kleinkinder zu faszinieren.

Bahnen der Zwei-Scheiben-Roller

Abb. 6: Die Bahnen der Schwerpunkte der Zwei-Scheiben-Roller sind schlangenähnliche Linien.
Ein einfaches Beispiel sind die am Rand eingeschnittenen Kreisscheiben des Konstruktionsspielzeuges Rondi (Abb. 8). Steckt man zwei der Scheiben bis zum Anschlag ineinander, ist die Abstandsbedingung ziemlich genau erfüllt. Der Hersteller hatte das allerdings nicht beabsichtigt.
Die englische Künstlerin A. Alley hat einen großen Zwei-Scheiben-Roller geschaffen und ihn ‘Rocking Toy’ genannt (Abb. 9). Hier ist die Abstandsbedingung nicht erfüllt. Das hat zur Folge, daß das Objekt nach einem Anstoß hin- und herwackelt.
 

Ensihammas

Abb. 7: Das finnische Kinderspielzeug Ensihammas (Größe » 6cm) ist ein Zwei-Kreis-Roller.

 

 

Rondi

Abb. 8: Mit dem Konstruktionsspielzeug Rondi (Größe » 2,5cm) läßt sich ebenfalls ein Zwei-Kreis-Roller zusammenstecken.

  

Rocking Toy

Abb. 9: Dieses künstlerische Objekt mit einer Größe von etwas über einem Meter wackelt hin und her.

Mit Bieruntersetzern (Bierfilze) lassen sich sehr gut Zwei-Scheiben-Roller bauen. Auch elliptische Bieruntersetzer eignen sich hervorragend. Mit meinem Koauthor C. Engelhardt konnten wir unseren Bedarf irgendwann in normalen Gaststätten nicht mehr befriedigen und schrieben an eine Brauerei. Die Reaktion war außerordentlich positiv. Wir bekamen mehrere hundert Bieruntersetzer und mehrere Kästen Bier ‘zur Förderung unserer Forschungsaktivitäten’.
Bei näherer Untersuchung der Rollbewegung ergibt sich, daß eine einbeschriebene Kugel mit dem Radius (b = kleine Halbachse der Ellipse) den ebenen Untergrund immer berührt (Abb. 10). Verfolgt man die Berührkurve auf dieser Kugel ergibt sich gerade eine sogenannte Tennisballkurve. In Abb. 11 ist diese Kurve als Schnitt eines hyperbolischen Paraboloids mit einer Kugel dargestellt. Von hier kann man tiefer in die Mathematik der Kegelschnitte eintauchen.

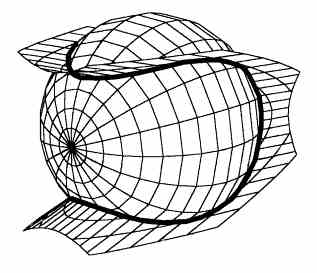
Berührkugel auf der Kugel

Abb. 11 (rechts): Die Berührkurve auf der Kugel läßt sich als Schnitt der Berührkugel mit einem hyperbolischen Paraboloid darstellen.

Berührkugel auf der Kugel
Verbindet man die Auflagepunkte eines Zwei-Kreis-Rollers sukzessive miteinander, erhält man einen ästhetisch aussehenden Körper (Abb. 12), den die Mathematiker als Torse bezeichnen. In diesem Fall ergibt sich ein konvexer Hüllkörper, der sich in der Ebene abwickeln läßt.
 

[Start-Seite] [Seite vor] [Seite zurück]

[Homepage Gebrüder Grimm]